Uvedených je niekoľko vybraných príkladov výsledkov aktivít v rámci základného geotermického výskumu:
1.
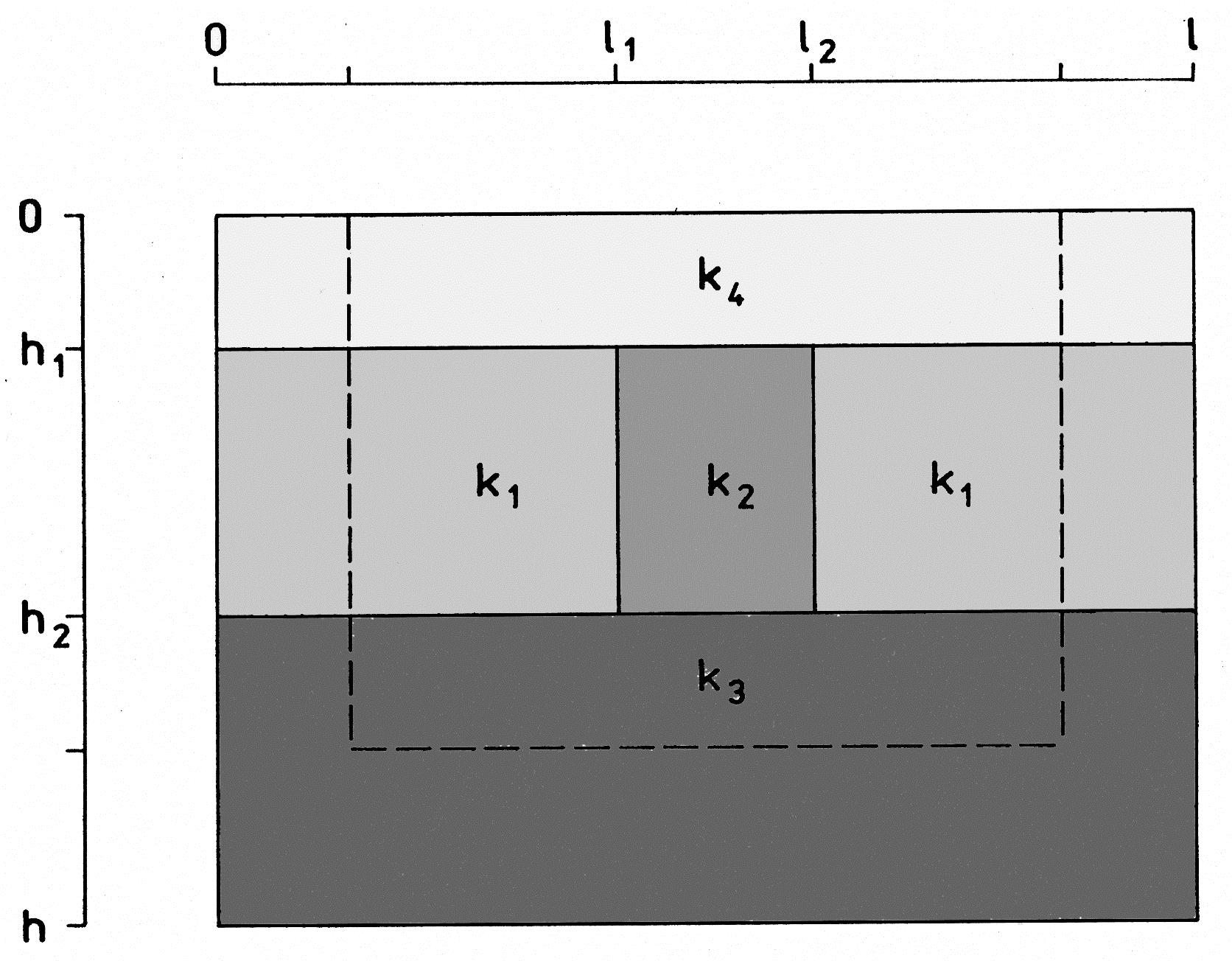
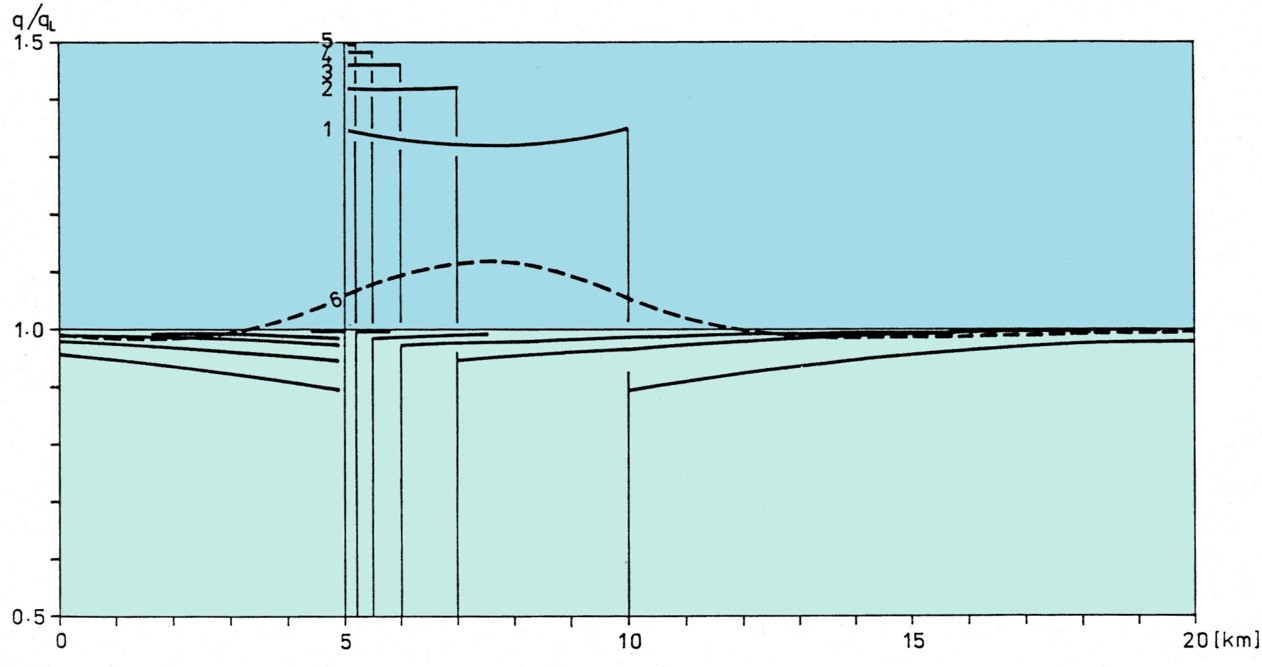
Základné úlohy refrakcie tepelného toku na jednoduchých štruktúrach s rôznymi kombináciami parametrov tepelnej vodivosti. Zobrazené sú rozloženia hustoty povrchového tepelného toku pre modely vertikálnej štruktúry s rôznou šírkou b = l₂ - l₁, s pokryvom ( h₁ = 0, plné čiary) a pre porovnanie aj bez neho (h₁ = 2000 m, čiarkovane). V uvedených modeloch sú fixované hodnoty k₂ / k₁ = 3.00/2.00, h₂ = 5000 m, k₂ = k₃. Mení sa hodnota b: pre 1 a 6 b = 5000; pre 2 b = 2000; pre 3 b = 1000; pre 4 b = 1000; pre 5 b = 500m. Rozloženia hustoty povrchového tepelného toku bez pokryvu majú skok nad hranicou anomálneho telesa a pokryv spôsobuje len lokálnu anomáliu bez skoku. Skok v rozložení pritom zodpovedá zmene v hodnotách tepelnej vodivosti. Zakrivenie grafov distribúcií je pritom spôsobené hlavne zmenami v rozložení teplotného poľa pre príslušné modely. Čím užšie je teleso tým menšie zmeny sú v teplotnom poli. To má napríklad uplatnenie pri interpretácii tepelných charakteristík (hustota tepelného toku a teploty) v okolí zlomových línií.
2.
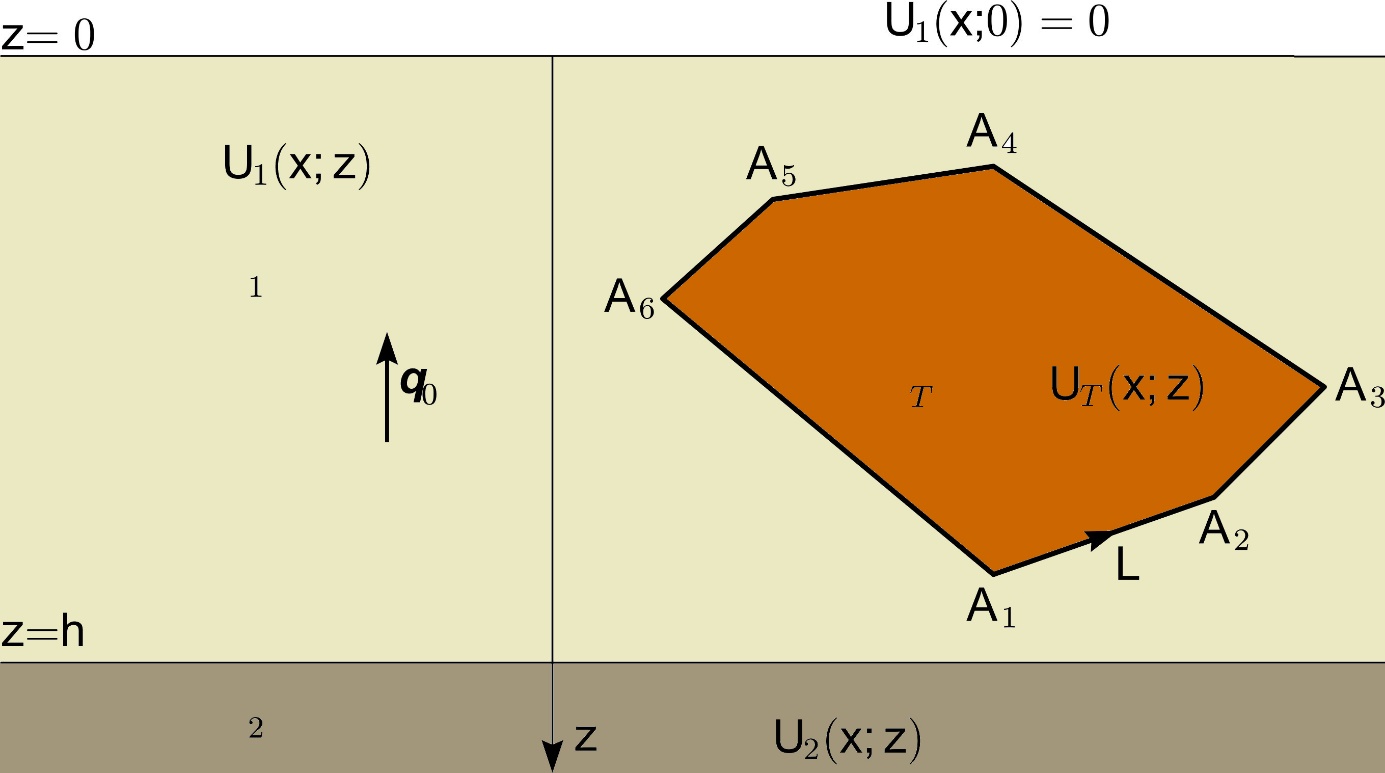
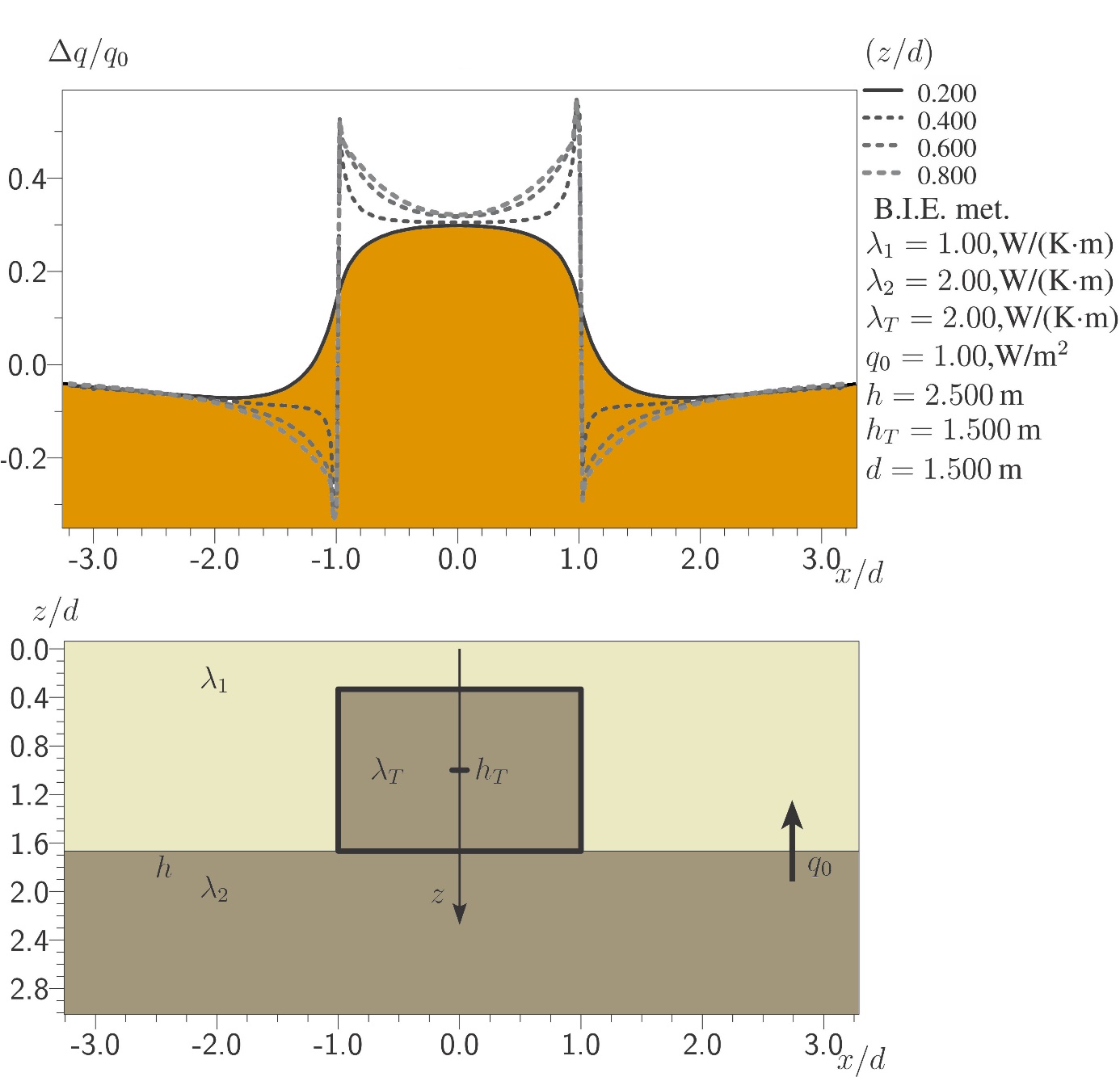
Rozloženie hustôt relatívneho povrchového tepelného toku a relatívneho tepelného toku na rôznych horizontálnych úrovniach pre refrakciu na 2D polygonálnom telese v dvojvrstvovej Zemi (vrchný obrázok).
Ukážka variantu modelového telesa s dotykom na hranici vrstiev (aproximujúceho refrakciu na hrásti s vertikálnymi bočnými stenami). Konfigurácia modelu a výsledky sú uvedené na spodných dvoch obrázkoch. Skoková zmena v distribúciách existuje iba na horizontálnych úrovniach prechádzajúcich hrásťou. Takéto modely sú využívané pre interpretáciu rozloženia teploty a vypočítaných hodnôt hustoty tepelného toku vo vrtoch ležiacich blízko telies s rozdielným koeficientom tepelnej vodivosti.
3.
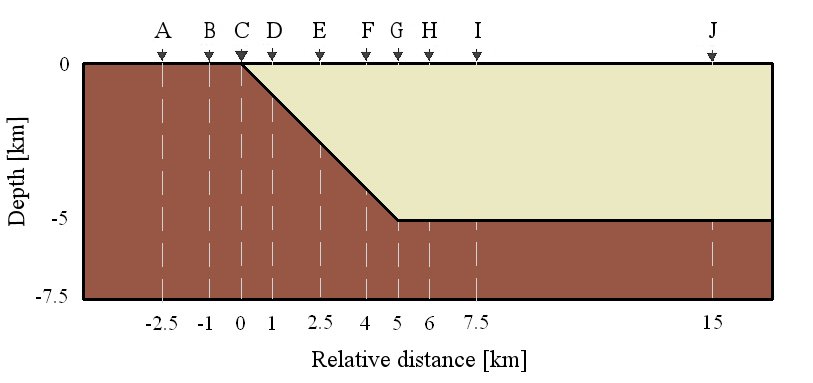
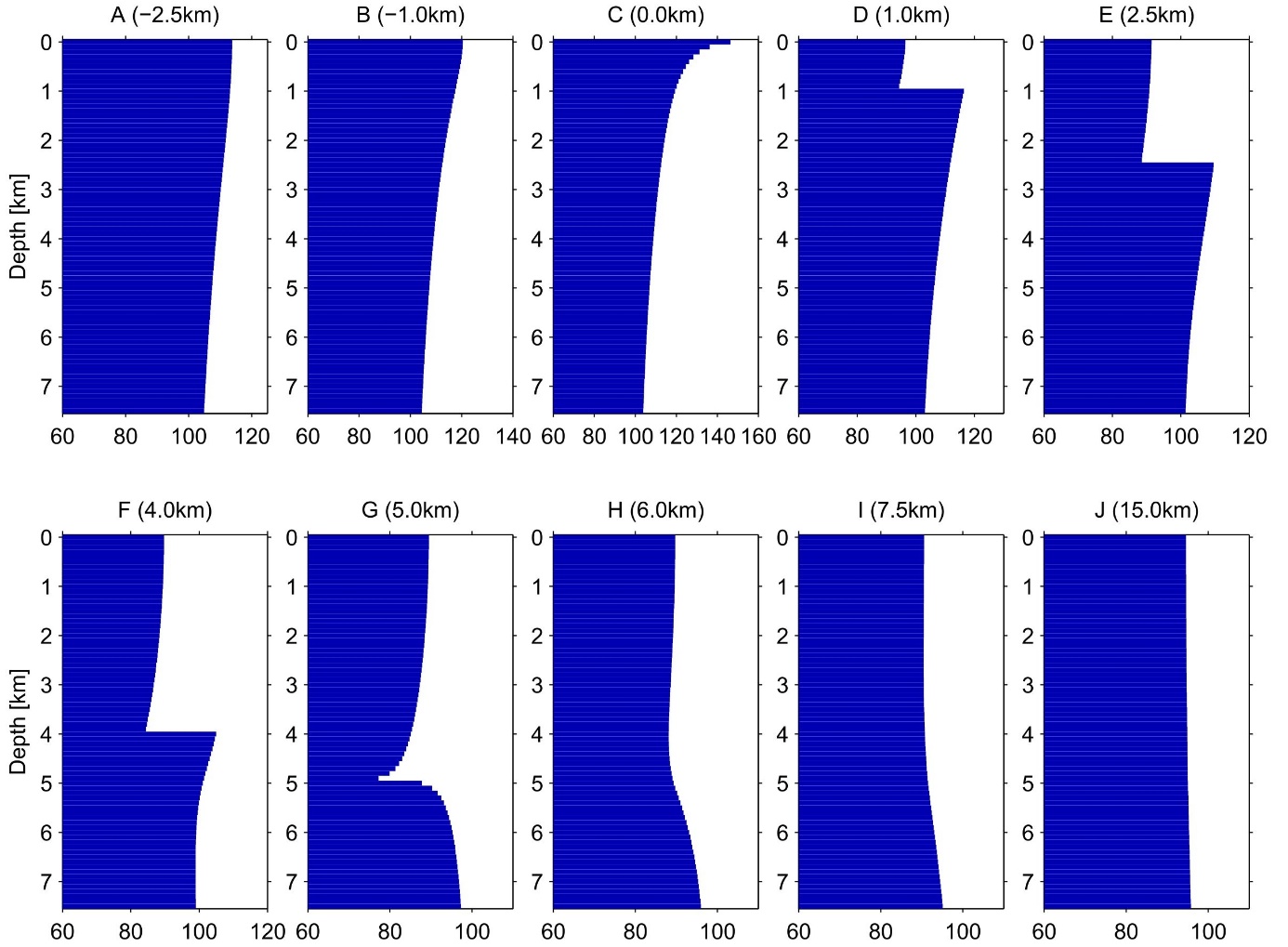
Vertikálne rozloženie vertikálnej zložky hustoty tepelného toku v referenčných bodoch A – J spôsobené refrakciou tepelného toku na okraji sedimentárneho bazéna (vrchný obrázok). Jednotlivé zobrazene krivky zodpovedajú rozloženiu vypočítaných hustôt tepelného toku (s krokom 100 metrov) vo vrtoch prechádzajúcich štruktúrou (spodný obrázok). Typickou je skoková zmena na šikmých rozhraniach horninových komplexov a vidieť vplyv horizontálneho prenosu tepla na štruktúre.
Výsledky majú veľký význam pri určovaní hodnôt tepelného toku blízko hranice sedimentárna výplň / podložie. Odhad refrakčných efektov je využívaný pre interpretácie rozloženia hustoty zemského tepelného toku blízko okraja sedimentárneho bazéna napríklad pri inverznej metóde postupného odkrývania v geotermickom modelovaní.
4.
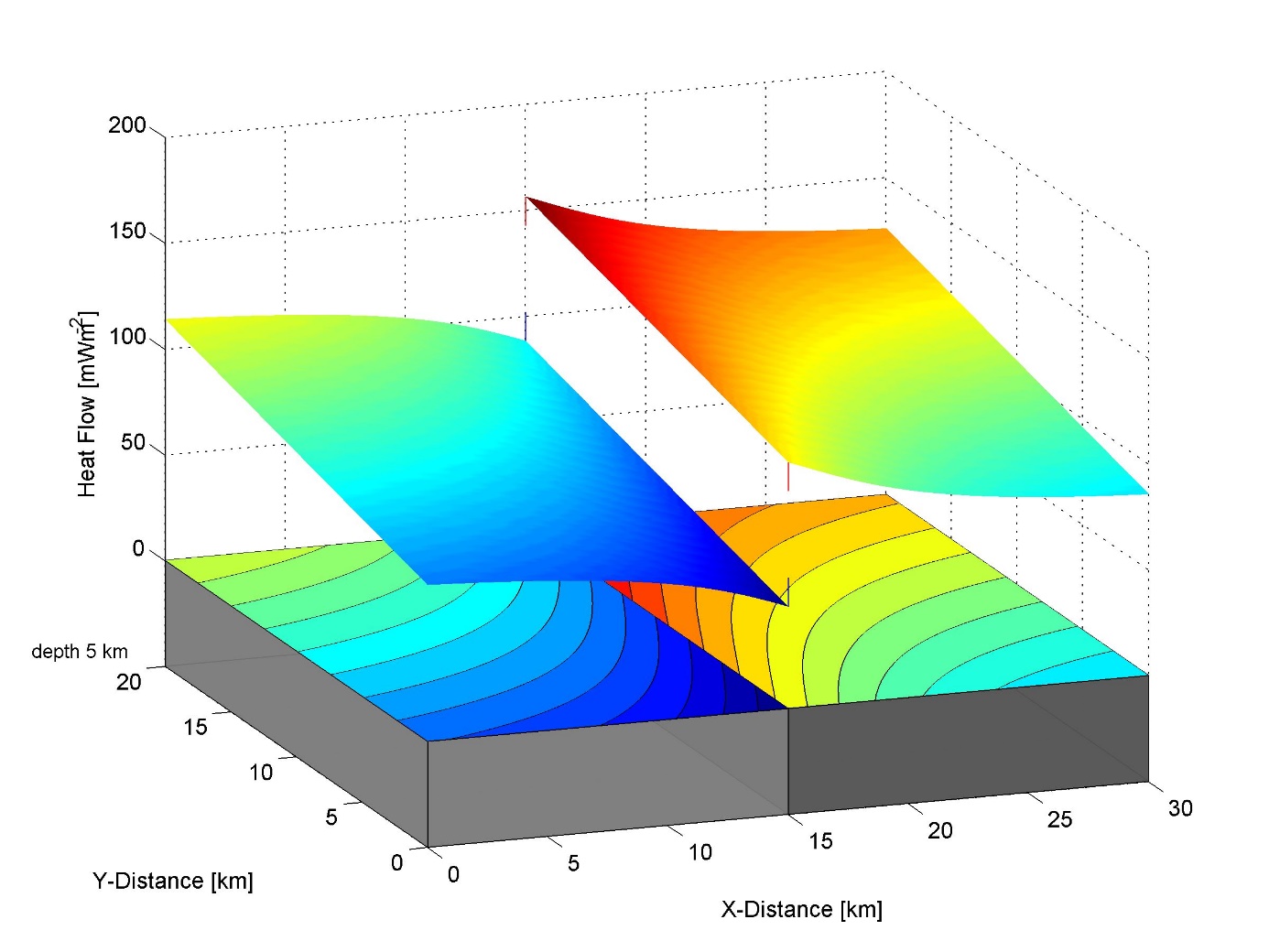
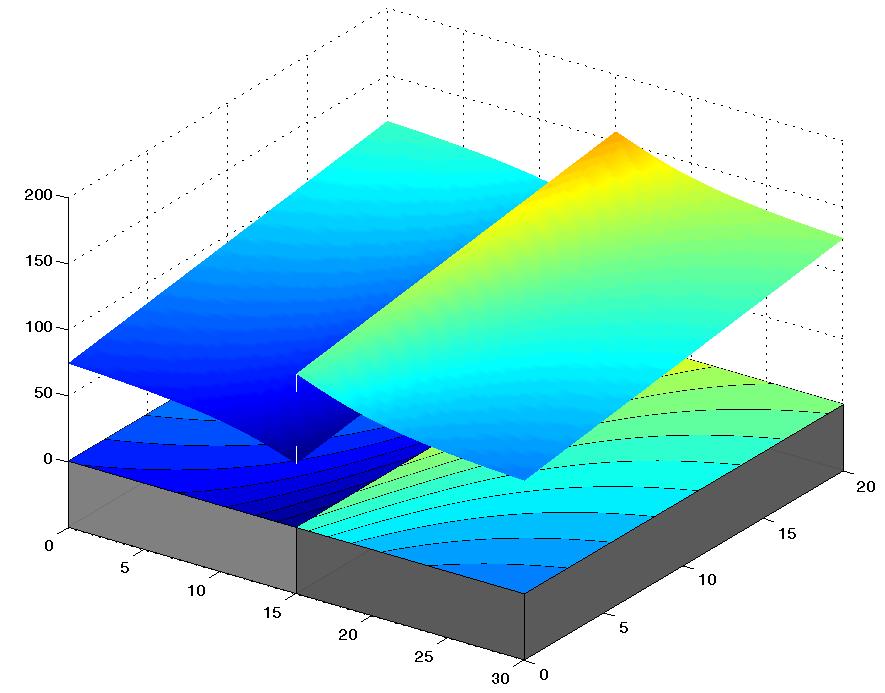
Skoková zmena v rozložení vertikálnej zložky hustoty tepelného toku spôsobená refrakciou toku na vertikálnom rozhraní s kontrastom v koeficiente tepelnej vodivosti a za predpokladu lineárneho nárastu hodnôt hustoty tepelného toku na dolnej hranici modelu pozdĺž roviny s kontrastom. Smery zobrazených 2D izolínií na oboch stranách od rozhrania nadväzujú (to zodpovedá spojitému rozloženiu teploty) avšak nad rozhraním existuje posun izolínií s rovnakou hodnotou (to je spôsobené skokovou zmenou koeficientu tepelnej vodivosti na rozhraní horninových komplexov). V uvedenom modeli je vodivosť horninových komplexov definovaná nasledovne: bledošedá - 2 W/m.K a tmavošedá - 3 W/m.K.
5.
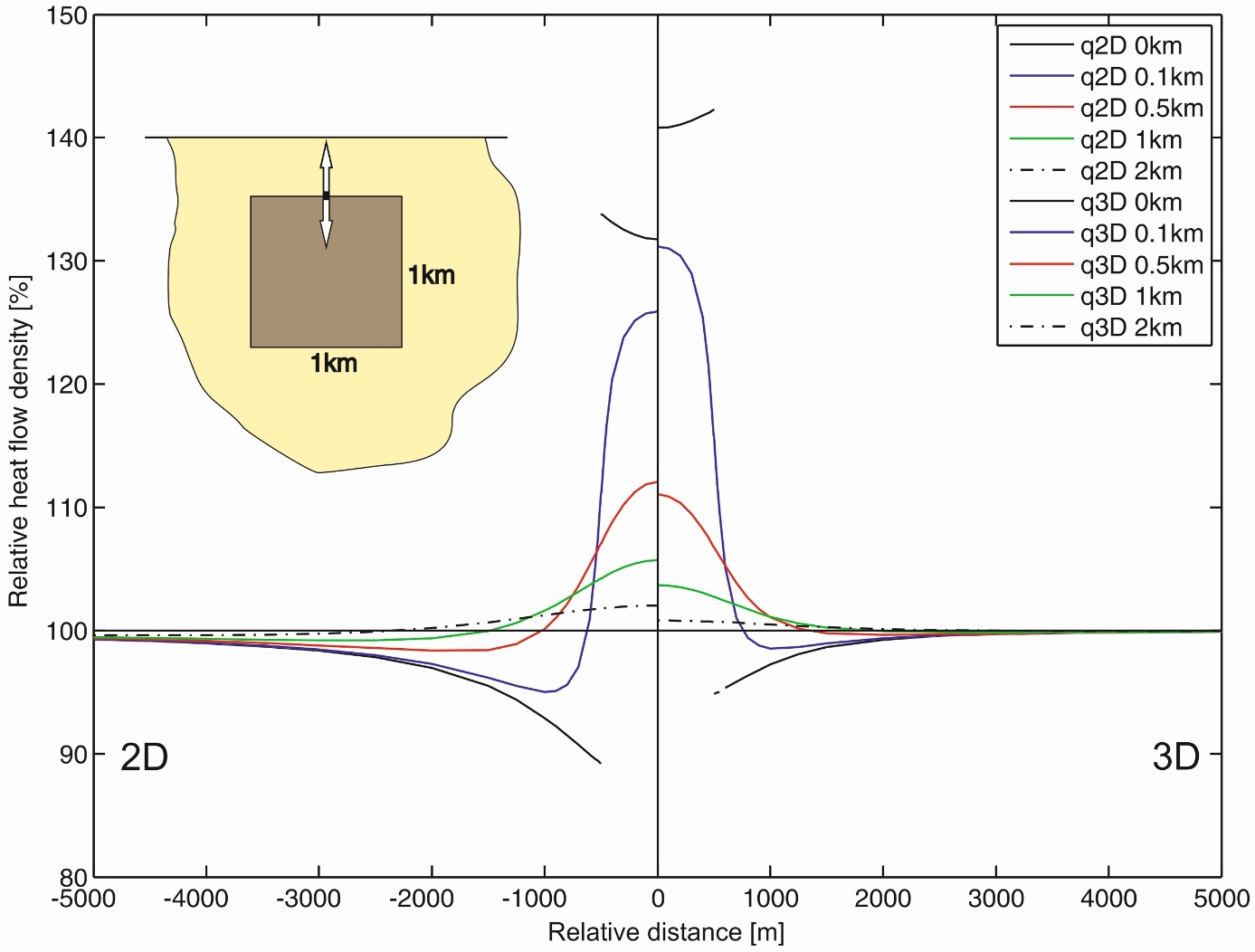
Porovnanie distribúcií relatívnych povrchových tepelných tokov pre refrakciu na 2D a 3D anomálnom telese umiestnenom v polpriestore na rôznych hĺbkach (uvedených v legende obrázku) hornej plochy telesa. Ľavá strana: 2D model s anomálnym hranolom štvorcového prierezu. Pravá strana: 3D model s anomálnou kockou. Výsledky výpočtov poskytujú zaujímavý zdanlivý paradox v rozložení hustoty povrchového tepelného toku: nad menším 3D telesom sú amplitúdy anomálií väčšie ako nad 2D telesom vždy ak je anomálne teleso blízko povrchu alebo sa dotýka povrchu. Je to špecifikum refrakčných anomálií spôsobené tým, že 3D teleso sústreďuje prúdočiary toku tepla z viacerých smerov. V modeloch s väčšou hĺbkou uloženia anomálneho telesa sa amplitúdy anomálií rozloženia tepelného toku v 2D a 3D prípade chovajú podobne ako v zdrojových úlohách.
6.
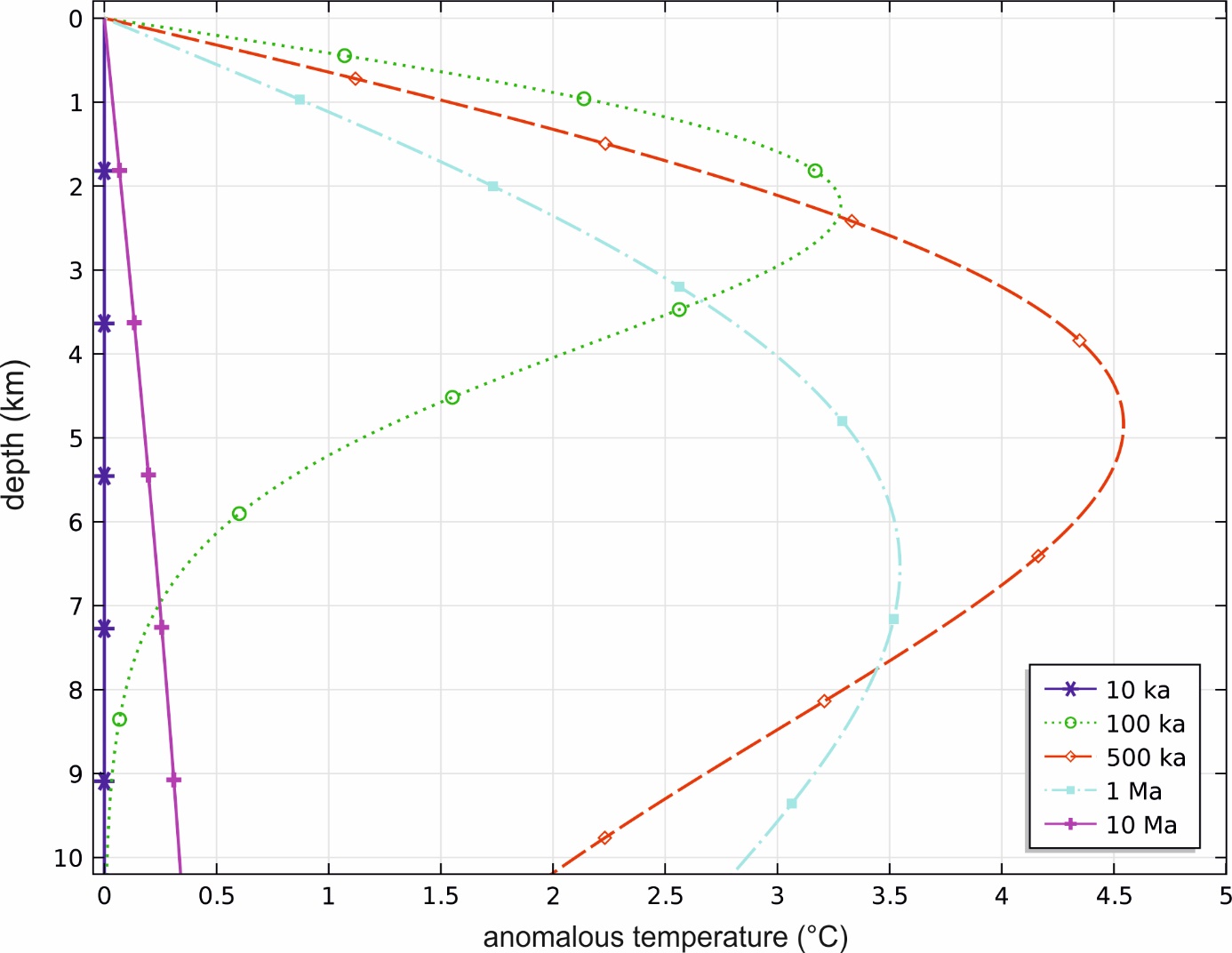
Časové zmeny rozloženia anomálnych teplôt s hĺbkou pre subvulkanické teleso v hĺbke 1 km. Mocnosť sillu telesa je približne 1 km.
Takéto odhady účinkov chladnutia magmatických telies sú využívané pri inverznej metóde postupného odkrývania v geotermickom modelovaní spolu s odhadmi refrakčných efektov.
Referencie
Majcin D., 1982: Mathematical models of stationary heat conduction. Contrib. Geophys. Geod., 13, 135-151.
Majcin D., 1993: Refraction of heat flow on the near-surface structures with thermal conductivity contrast. Contributions - Slovak Academy of Sciences, Geophysical Institute 22, 67-80.
Majcin D., Polák Sz. 1995: Refraction of heat flow near the border of the sedimentary basins with topography. Contrib. Geophys. Geod., 25, 99-112.
Tsvyashchenko V. A., Majcin D., Kutas R. I., Tsvyashchenko A. V., 2000: Modelling stationary thermal field of heterogeneous environment. Doklady NAS of the Ukraine, 4, 134–138 (in Russian).
Hvoždara M., Majcin D., 2009: Geothermal refraction problem for 2-D body of polygonal cross-section buried in the two-layered earth. Contributions to Geophysics and Geodesy, vol. 39/4, 301-323.
Hvoždara, M., Majcin D., 2011: Refraction effect in geothermal heat flow due to a 3D prismoid, situated in the substratum of two-layer Earth. Contributions to Geophysics and Geodesy, vol. 41/3, 211-233.
Majcin D., Bilčík D., Hvoždara M., 2012: Refraction of heat on subsurface contrast structures – the influence both on geothermal measurements and on interpretation approaches. Contributions to Geophysics and Geodesy, vol. 42/2, 133-159.
Hvoždara M., Majcin D., 2013: Geothermal heat flux anomaly due to a 3D prismoid situated in the second layer of a three-layered Earth. Contributions to Geophysics and Geodesy, vol. 43/1, 39-58.
Majcin D., Bilčík D., Kutas R.I., Hlavňová P., Bezák V., Kucharič Ľ., 2014: Regional and local phenomena influencing the thermal state in the Flysch belt of the northeastern part of Slovakia. Contrib. Geophys. Geod., 44/4, 271–292.