Oddelenie gravimetrie a geodynamiky

Jaroslava Pánisová¹ a Roman Pašteka²

1 Geofyzikálny ústav, Slovenská akadémia vied, Bratislava, Slovensko, Táto e-mailová adresa je chránená pred spamovými robotmi. Na jej zobrazenie musíte mať zapnutý JavaScript.
2 Katedra aplikovanej a environmentálnej geofyziky, Univerzita Komenského, Bratislava, Slovensko

Mikrogravimetria

Mikrogravimetria je založená na vysoko presnom meraní a interpretácii veľmi malých variácií v tiažovom poli Zeme. Merané tiažové údaje sú ovplyvnené zmenami v zemských slapoch, zemepisnej šírke, nadmorskej výške a okolitej topografii. Interpretujeme preto len anomálnu časť meraného tiažového zrýchlenia. Tvoria sa tzv. Bouguerove anomálie, kde sú odstránené účinky všetkých týchto negeologických faktorov. Metodika mikrogravimetrie bola detailne popísaná v [1, 5].

Antropogénna korekcia

 Keď sú mikrogravimetrické prieskumy realizované vo vnútri alebo v blízkosti veľkých stavieb, ich prítomnosť spôsobuje znižovanie meraného tiažového poľa. Pojem „antropogénna korekcia“ (tzv. korekcia na účinok múrov) obsahuje všetky dodatočné korekcie, ktorými sa odstraňujú účinky budov a známych podzemných priestorov [1, 4]. Štandardný spôsob ich výpočtu je založený na aproximácii múrov systémom jednoduchých geometrických telies (kvádre alebo 3D vertikálne hranoly s polygonálnym prierezom). V novom prístupe je model skúmanej budovy zrekonštruovaný z fotografií v softvéri PhotoModeler. Výstupom je 3D mnohostenné teleso v zvolenej súradnicovej sústave [4].

Program Polygrav

Gravitačný účinok homogénneho mnohostena, ktorého povrch je popísaný nepravidelnou trojuholníkovou sieťou (TIN), sa počíta v programe Polygrav sumáciou integrácií pozdĺž čiarových elementov jednotlivých trojuholníkov použitím rovnice odvodenej v [3]. Súbor, exportovaný z PhotoModeleru v tzv. „raw“ formáte, slúži ako priamy vstup do nášho programu. Tento súbor obsahuje priestorové súradnice všetkých bodov a povrchových trojuholníkov, z ktorých je vytvorené exportované teleso. Topológia modelu je tvorená a kontrolovaná užívateľom. Program Polygrav kontroluje a oznamuje nasledujúce udalosti: 1) existenciu viacerých identických trojuholníkov, 2) chybné poradie vrcholov na niektorej stene a 3) chýbajúce trojuholníky. Telesá rôznych hustôt sa importujú a počítajú oddelene.

Príklad

Neskororománsky kostol Narodenia Panny Márie sa nachádza v Horných Krškanoch blízko Nitry na západnom Slovensku. Bol postavený v druhej polovici 13. storočia. Neskoršie prestavby odrážajú prvky gotického a barokového slohu. V roku 2008 bola počas reštaurátorských prác v presbytériu objavená vzácna gotická freska zo 14. storočia. Geofyzikálny prieskum kostola [4] sa uskutočnil v rámci medzinárodnej letnej školy archeo-geofyziky INCA 2009 pre študentov geofyziky a archeológie [6].

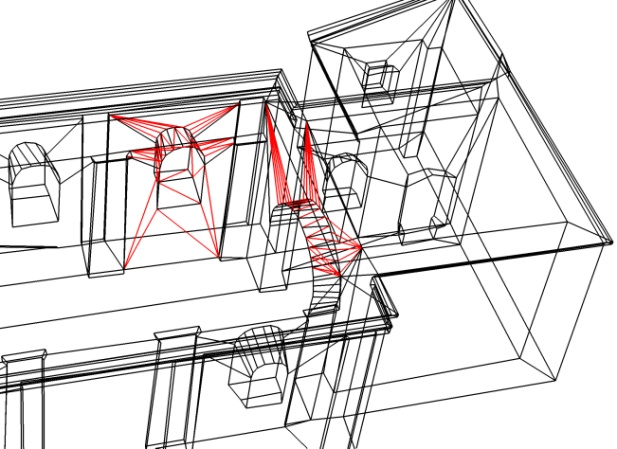
Obr. 1: Dva rôzne pohľady na digitálny model v softvéri PhotoModeler.

Fotogrametrické spracovanie

 V roku 2010 bol tento kostol zdokumentovaný konvergentnou fotogrametriou pre účely rekonštrukcie jeho priestorového modelu. Na snímkovanie bol použitý digitálny fotoaparát Canon EOS 450D, ktorý bol kalibrovaný na priestorovom kalibračnom poli v priestoroch Stavebnej fakulty STU [2]. Model kostola bol transformovaný do geodetického súradnicového systému pomocou 37 vlícovacích bodov označených kódovými terčíkmi. Pre úspešnú rekonštrukciu interiéru bolo potrebné tachymetricky zamerať ďalších 90 bodov, ktoré boli zakryté vnútorným vybavením kostola. Reálna presnosť modelu (empirická stredná chyba) dosiahla 6.5 cm. Na obr. 1 vľavo je znázornený priestorový digitálny model kostola bez strechy s originálnymi textúrami v softvéri PhotoModeler. Obr. 1 vpravo znázorňuje obrysy vybranej časti výsledného modelu kostola. Červené čiary boli použité na ukážku triangulácie na niekoľkých vybraných plochách. Výsledný model kostola (obr. 1) sa skladá z 939 bodov a 1902 trojuholníkov.

Tabuľka 1: Vstupné parametre použité v syntetickom modelovaní

Presnosť antropogénnej korekcie

Štandardná neistota antropogénnej korekcie je závislá od presnosti určenia geometrie budovy a od presnosti odhadu jej priemernej hustoty. Zmenou parametrov syntetických modelov (viď Tabuľka 1) bola určená presnosť antropogénnej korekcie, normovaná na referenčný model (viď pôdorys na obr. 2a). Maximálna neistota antropogénnej korekcie, odhadnutá empiricky zo syntetického modelovania, je ±7 μGal (obr. 2a). Do vzdialenosti ≈1.0 m od múrov (1.5 m v prípade rohov budovy) je možné identifikovať len anomálie hľadaných štruktúr, ktoré majú amplitúdu väčšiu ako 7 μGal. Keďže je stredná chyba meranej tiaže zvyčajne nižšia ako 4 μGal, presnosť modelov zrekonštruovaných pomocou softvéru PhotoModeler by nemala presiahnuť 1–2 cm. Analýza presnosti počítaných antropogénnych korekcií nebola možná v štandardnom prístupe.

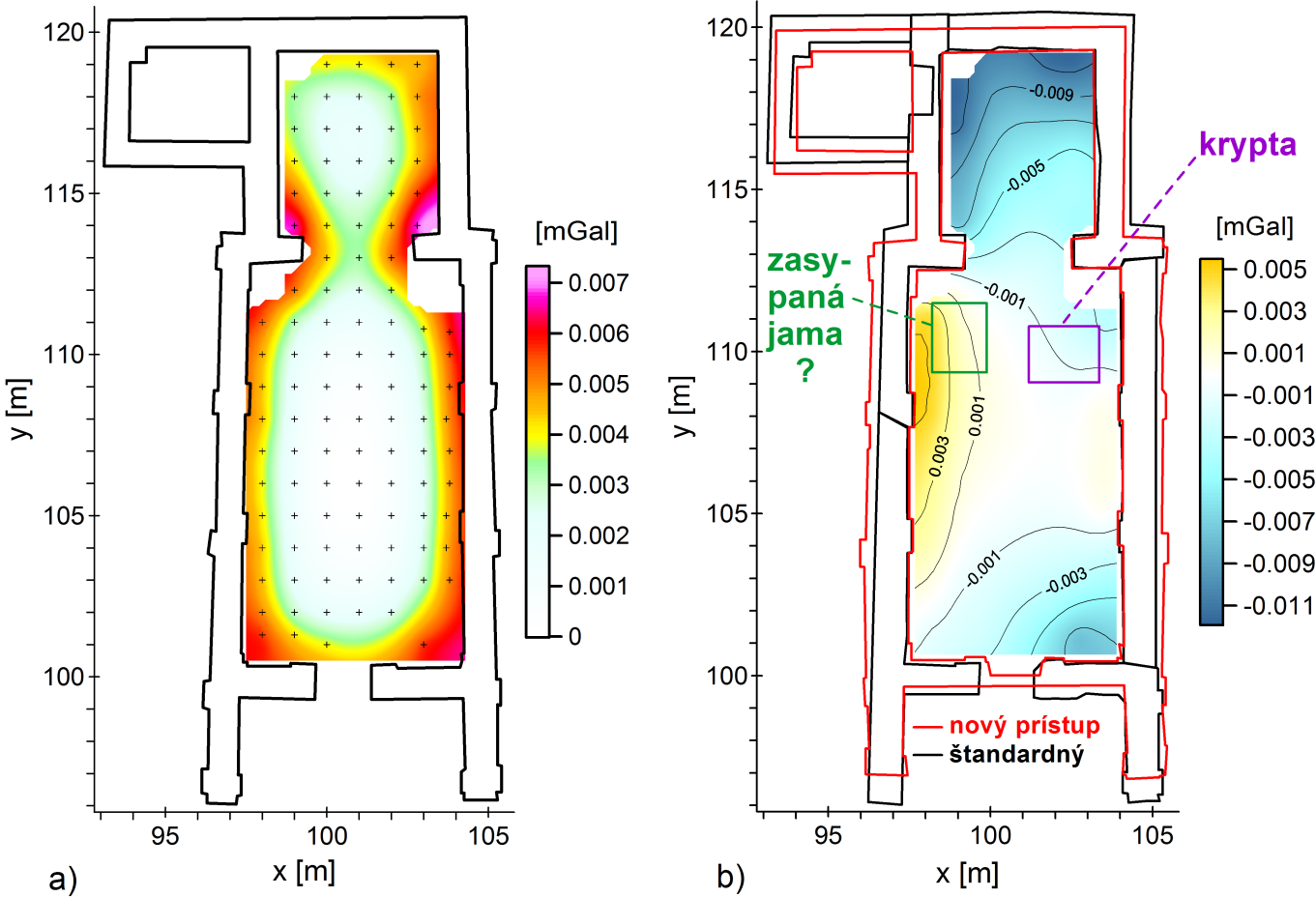
Obr. 2: a) Štandardná neistota antropogénnej korekcie odhadnutá zo syntetického modelovania múrov kostola. b) Porovnanie dvoch pôdorysov zobrazené spolu s rozdielovou mapou antropogénnych korekcií: nový mnohostenný model verzus starý model tvorený hranolmi.

Porovnanie prístupov

Pôdorysy dvoch modelov kostola získané rôznymi prístupmi v nezávislých programoch sú porovnané na obr. 2b. V štandardnom prístupe boli hlavné múry budovy aproximované v programe Potent (Geophysical Software Solutions) pomocou 5 vertikálnych hranolov s polygonálnym prierezom a odhadnutou hustotou 1.8 g/cm³. Pôdorys „štandardného prístupu“ znázornený čiernou farbou sa takmer zhoduje s pôdorysom „nového prístupu“ (červená čiara) vo vnútorných priestoroch kostola, ale vonkajšie steny sa tvarovo líšia, čo zapríčinilo maximálne rozdiely 30–40 cm v hrúbke múrov.

Nová metóda výpočtu antropogénnej korekcie umožnila začleniť do modelu oblúkové okná a lomený oblúk (obr. 1 vpravo). Toto nebolo možné v aproximácii vertikálnymi hranolmi. Rozdiely v rozsahu +5 μGal až –11 μGal medzi antropogénnymi korekciami vypočítanými z výstupného súboru zo softvéru PhotoModeler a modelu vytvoreného z hranolov (Potent) pochádzajú hlavne z tvarového nesúladu hlavných stien (mapa na obr. 2b). Z pohľadu interpretácie je týmito rozdielmi ovplyvnená len vyplnená dutina.

Závery

 Naša nová metóda poskytuje vysokú presnosť počítaných účinkov stavieb, čo prináša možnosť odhaliť dutiny nachádzajúce sa v tesnej blízkosti umelo vytvorených štruktúr. Takéto vylepšenie môže pozitívne prispieť k tvorbe presnejších máp Bouguerových anomálií a ich interpretácii. Trojrozmerná rekonštrukcia historických stavieb pomocou metód blízkej fotogrametrie zároveň predstavuje hodnotný príspevok k dokumentácii kultúrneho dedičstva.

Literatúra

1. Blížkovský M. 1979. Processing and applications in microgravity surveys. Geophysical Prospecting 27(4): 848–861.

 2. Fraštia M. 2005. Possibilities of using inexpensive digital cameras in applications of close-range photogrammetry. Slovak Journal of Civil Engineering 8(2): 20–28.

 3. Götze HJ, Lahmeyer B. 1988. Application of three-dimensional interactive modeling in gravity and magnetic. Geophysics 53(8): 1096–1108.

 4. Panisova J, Pašteka R, Papčo J, Fraštia M. 2012. The calculation of building corrections in microgravity surveys using close range photogrammetry. Near Surface Geophysics 10(5): 391–399. DOI: 10.3997/1873-0604.2012034.

 5. Pašteka R, Pašiaková M, Panisova J, Zahorec P, Papčo J, Fraštia M, Wunderlich T, Terray M. 2013. Microgravity method in archaeological prospection: methodical comments on selected case studies from Slovakia. SEG Technical Program Expanded Abstracts 2013: 1966–1971. DOI: 10.1190/segam2013-0299.1.

 6. Rabbel W, Serif B, Pašteka R. 2010. The INCA International Course on ArchaeoGeophysics – an EU intensive program of teaching interdisciplinarity in science. EGU General Assembly 2010, Vienna, Austria, Geophysical Research Abstracts 12, 14041.

pdf verzia na stiahnutie